Julen närmar sig med stormsteg, och det är hög tid för kägelsnitt.
Ett kägelsnitt är ett snitt genom en kägla, eller cirkulär kon för att vara mer exakt.
Jag hittar en av SFDPW:s (San Francisco Department of Public Works) övergivna trafikkoner i ett gathörn
och tar hem den.
Jag sätter igång med snittet, men det visar sig att konen är gjord av mjuk och seg plast, som är svår att ta sig igenom.

Men till sist går det, och jag kan rita av konturen till en ellips. (Inte vacker precis).
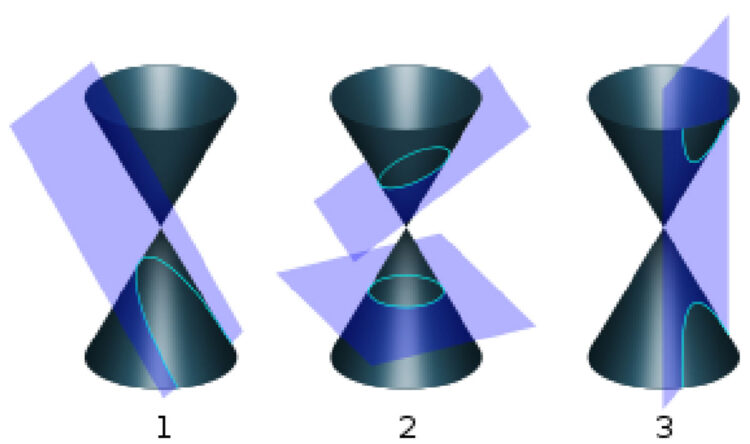
Apollonius av Perga (född ca 262 fKr i Anatolien nuvarande Turkiet och död ca 190 f Kr i Alexandria Egypten, där han verkade), redde ut kägelsnitten i åtta böcker. De fyra senaste försvann spårlöst, men tre av dem hittades senare i en arabisk översättning. Verket hette just Kägelsnitt. Dess grekiska namn hittar jag inte, men på engelska Conics. De tre typerna av kägelsnitt ses i bilden ovan, där de illustreras med en dubbelkon.
Parabeln, som fås om ett plan skär parallellt med generatrisen, d v s konens sidolinje. Det skär antingen den nedre eller den övre konen men inte båda.
Ellipsen, som fås när planet skär av konen snett. Är snittet horisontellt, blir det en cirkel.
Hyperbeln, som fås när planet skär både den nedre och den övre konen. Den består alltså av två delar. Snittet behöver inte vara vertikalt.
Apollonius påvisade många märkliga egenskaper hos kägelsnitten. De har t ex ”brännpunkter” med vars hjälp de kan definieras.
Skickar man iväg en ljusstråle från den vänstra brännpunkten, så reflekteras den alltid till den högra brännpunkten och vice versa. På ”Exploratorium” i San Francisco, och säkert många andra ”upptäckarmuseer” kan man testa det i stor skala.

Ovan ses den ena änden av en ellipsoid med den andra uppställd långt till höger. Står man i brännpunkten och viskar in i ellipsoiden, reflekteras ljudet perfekt till den andra brännpunkten, där en lyssnare kan höra det.
En annan egenskap är att avståndet från ena brännpunkten till den andra via ellipsens periferi är konstant. Vi kan därför definiera ellipsen som ”Orten för en punkt från vilken summan av avstånden till två givna (bränn)punkter är konstant”. Så nu kan vi rita en ellips med hjälp av ett snöre (= summan av avstånden) och två häftstift. Fäst snörets ändpunkter i de två häftstiften. Håll det sträckt med pennan och rita.
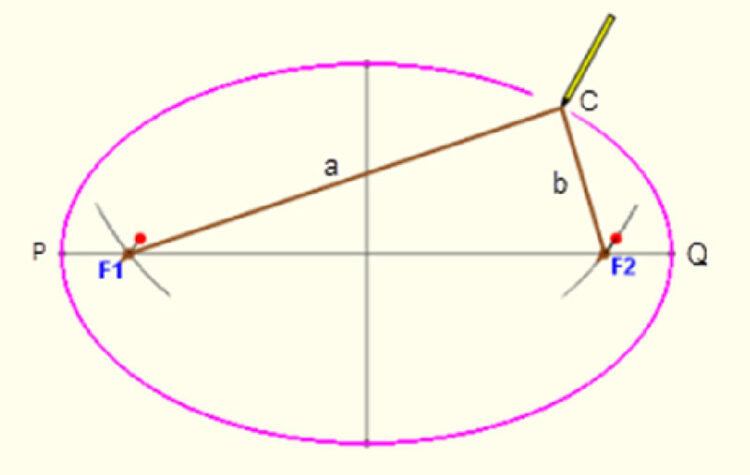
Ju närmare varandra häftstiften (brännpunkterna F1 och F2) är, desto rundare blir ellipsen.

Längre avstånd mellan brännpunkterna ger en smalare ellips, som den gula i bilden till höger.
Parabeln
Det enklaste är nog att göra som Apollonius: Köp en frigolitkon i närmaste hobbybutik. Såga itu den parallellt med sidolinjen, generatrisen. Rita dess kontur på ett papper. Men det finns också ett annat sätt.
Bind det röda snörets ena ände nära vinkelhakens spets och den andra i spiken/parabelns brännpunkt
(krysset i bilden).
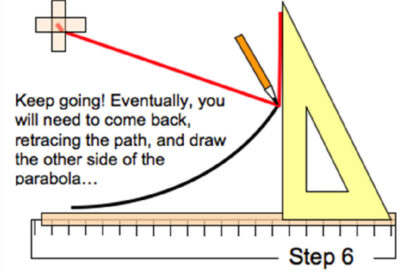
Den s k ”verkligheten”


Låt vinkelhaken glida längs papprets kant samtidigt som du håller snöret sträckt längs vinkelhakens sida. Här är det bra att ha tre händer. Fortsätt med vänstra sidan.
Parabeln är nog mest känd som konturen av en parabolantenn. Parallella strålar som träffar parabolen reflekteras alla till brännpunkten och sedan ut samma väg de kom. Detta visste Apollonius för 2.200 år sedan.
Två parallella strålar kommer in, reflekteras genom fokus och ut.
Spegeln i ett teleskop består förstås bara av den allra understa delen av parabolen ovan. Precis som att alla cirklar ser likadana ut, är ”likformiga”, så är också alla parabler likformiga. Zoomar man in eller ut, kan alla parabler fås att täcka varandra.
Hyperbeln
Hyperbeln kan precis som ellipsen definieras med hjälp av sina brännpunkter. Men i stället för ”summa” är det ”skillnad” som gäller. Hyperbeln är ”orten för en punkt vars avstånd till två givna punkter har en konstant skillnad”.
Hyperbeln närmar sig alltmer sina två styrlinjer eller assymptoter ju längre ut den går.
Därmed är det dags för dragkedjan
En spik (brännpunkt) genom dragkedjans ände och en annan en bit upp på den andra delen. Skillnaden! Sätt pennan genom dess (vad heter det?), och sedan öppnar man (eller stänger) dragkedjan, håller den spänd och ritar på en gång. Men här börjar materien protestera och tålamodet tryta.

Det finns ett andra sätt med sugrör, eller f d kulspetspenna som i bilden nedan, i stället för dragkedja, men det får bli överkurs:

Om ni, som Apollonius, saknar tillgång till sugrör, dragkedjor och kulspetspennor, så går det lika bra att såga itu frigolitkoner.
Apollonius skrev många andra böcker, men de är alla försvunna. Man har vaga idéer om vad de handlade om från samtida referenser. Mycket av den grekiska matematiken överlevde tack vare att den översattes till arabiska och långt senare vidareöversattes till latin.
”Although a fragment has been found of a thirteenth century Latin translation from the Arabic, it was not until 1661, that Giovanni Alfonso Borelli and Abraham Ecchellensis made a translation of Books 5-7 into latin. Although they used Abu ’l-Fath of Ispahan’s Arabic version of 983, which was preserved in a Florentine manuscript, most scholars now agree that the best Arabic renderings are those of Hilal ibn Abi Hilal for Books 1-4 and Thabit ibn Qurra for Books 5-7.” (https://www.newworldencyclopedia.org/).

I Europa hände inte så mycket de närmaste etttusenåttahundra åren. Men då klev Johannes Kepler (1571–1630) in på scenen. Han hade läst Apollonius skrifter och lärt sig om kägelsnitten, och det började röra på sig. Kepler kunde med hjälp av dansken Tycho Brahes (född på Knutstorps slott i Skåne 1546 och död i Prag 1601) tusentals noggranna mätningar på ön Ven i Öresund visa att planeterna rörde sig i elliptiska banor runt solen. Kägelsnitten fanns alltså inte bara som en geometrisk konstruktion av smarta greker, utan kunde beskådas lite varstans ute i världsrymden.
År 1687, när alla ovan nämnda herrar var döda, lät Isaac Newton (1643–1727) publicera sin Philosophiæ Naturalis Principia Mathematica, som beskrev hans tre rörelselagar samt, inte minst, den universella gravitationslagen (och mycket annat). Med dessa lagar följer att en himlakropp som kretsar kring en annan himlakropp måste röra sig i en elliptisk bana. Kommer den instörtande med tillräckligt hög hastighet som t ex den komet som Tycho Brahe gjort positionsmätningar på mellan 13/11 1577 och den 26/1 1578, så följer den dock en parabel eller hyperbel. Med hjälp av dessa mätningar vet man att C1587 passerade långt innanför Merkurius bana och att dess avstånd från solen nu är mer än tio gånger avståndet till Neptunus. Den väntas aldrig återkomma. Tycho var den siste astronomen som arbetade utan teleskop, med blotta ögat. Inte förrän 1610 skulle Galileo Galilei för första gången se himlen genom sin stjärnkikare.

Den rör sig i en mycket brant bana mot planetbanorna. Dessa är mycket nära cirkulära. Utom Merkurius, vars perihelium (punkten närmast solen) är 46 miljoner km och aphelium är 70 Mkm. Dvärgplaneten Pluto har också en klart elliptisk bana (ej markerad i bilden) som ibland korsar Neptunus bana.
Näste man heter Rene Descartes (1596–1650) . Han introducerade det Cartesiska koordinatsystemet, alltså en graderad x- och y-axel vinkelrätt mot varandra i sitt verk, La Géométrie år 1637. I detta koordinatsystem placerade han geometriska figurer. Därmed var den analytiska geometrin uppfunnen, en syntes av klassisk geometri och algebra. Han bestämde att okända storheter skulle betecknas med x och y, medan kända storheter skulle kallas a, b, c o s v. Det var också han som började skriva potensen på ett tal som t ex 34, ”tre upphöjt till fyra” (3x3x3x3 = 81).
Exempel: Placera en cirkel med radien r mitt i det cartesiska koordinatsystemet. Rita in en rätvinklig triangel med hypetonusan r och de andra sidorna x och y. Enligt Pythagoras sats, känd sedan några tusen år tillbaka, är då x2 + y2 = r2 , och vi har cirkelns ”ekvation” eller en algebraisk ”formel” som beskriver cirkeln, d v s ”orten för en punkt med konstant avstånd till en fix punkt”. Kägelsnittens ekvationer är något, men inte mycket, mer komplicerade.
Plötsligt kan vi beräkna en massa ting utan att rita eller mäta. Ställ dig t ex några pinnar upp på en stege som står nästan lodrätt mot väggen. Om nu stegen börjar glida mot golvet och väggen, kommer dina fötter, när de träffar golvet, att ha beskrivit en fjärdedels ellips. Vilket ju är intressant att veta om du hamnar på akuten.
Men med analytisk geometri kan vi beräkna den fjärdedels ellipsen utan att sätta foten på någon stege. Eller rotera en gryta halvfull med vatten. Ju snabbare rotation, desto högre upp på grytans vägg når vattnet. Ytan får formen av en paraboloid, som en parabolantenn, alltså. Det är en metod som har använts för att tillverka reflektorn till stora spegelteleskop. Smält glas, som långsamt får stelna, i stället för vatten. Så kallade zenitteleskop har tillverkats, där spegelytan består av roterande kvicksilver.
Medan kägelsnittets ellips har ekvationen x2/a2 + y2/b2 = 1, så finns det en lite tillplattad ”superellips” som
har ekvationen x4/a4 + y4/b4 = 1. Det är denna form som fontänen/rondellen på Sergels torg i Stockholm har. Dansken Piet Hein (1905–1996) låg bakom iden.
Slutord
Descartes mest kända yttrande är ”Je pense, donc je suis”, ”Cogito ergo sum” i latinsk översättning. ”Jag tänker, därför är jag”. Eller i Karl-Alfreds (Popeye Charlie) amerikanska tolkning: ”I am what I am and that’s all I am.”
Decartes rekryterades av drottning Kristina år 1649 för att undervisa henne om vetenskap, filosofi och kärlek. Hans ekonomi var usel och akademiker, präster och diverse potentater på kontinenten var efter honom, så han tog jobbet, något han snart skulle ångra. Den 22-åriga drottningen jagade honom ur sängen och tvingade honom att inställa sig för dagens lektion klockan fem på morgonen i sitt kalla slott, som var dåligt vinterbonat. Hon begrep sig inte på hans rationalism och logiska resonemang och tyckte snart illa om honom.
Descartes var varken imponerad av drottningen eller det kalla andliga och fysiska klimatet i hennes huvudstad. Han bestämde sig för att flytta tillbaks till Holland, men försent. Snart blev denne nyss så pigge fransman sjuk i lunginflammation och dog i februari 1650, ca fyra månader efter sin ankomst till Stockholm. Han begravdes bland dödfödda och föräldralösa barn i stadens utkant, numera Adolf Fredriks kyrkogård. Efter några årtionden grävde fransmännen upp honom och tog kvarlevorna till Paris, där de efter några flytt hamnade i kyrkan Saint-Germain-des-Près. Minus hans huvud, som finns på ett museum i samma stad.
360 år efter Descartes dök en annan intet ont anande sanningssökare upp i Stockholm. Kungligheterna visade inget intresse för honom, men han råkade illa ut ändå. Till skillnad från Descartes lyckades han dock ta sig ut ur staden och landet med livet i behåll. Grattis Julian och lycka till!


















Tychos komet heter alltså C1577, som framgår av bilden. Jag skrev fel i texten. ”C” betyder ”icke-periodisk”, och 1577 står för årtalet när den registrerades. Periodiska kometers namn börjar med ”P”.