Det så kallade ”gyllene snittet” är känt sedan urminnes tider, och kan definieras så här: Gyllene snittet är det förhållande som erhålls när en sträcka delas i en längre del a och en kortare del b så att ”den kortare delen b förhåller sig till den längre delen a så som a förhåller sig till hela sträckan a+b”.
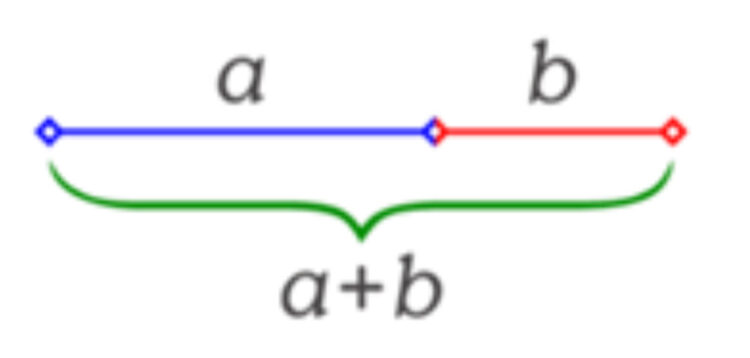
Ett sätt att illustrera förhållandet är att rita rektangeln nedan.
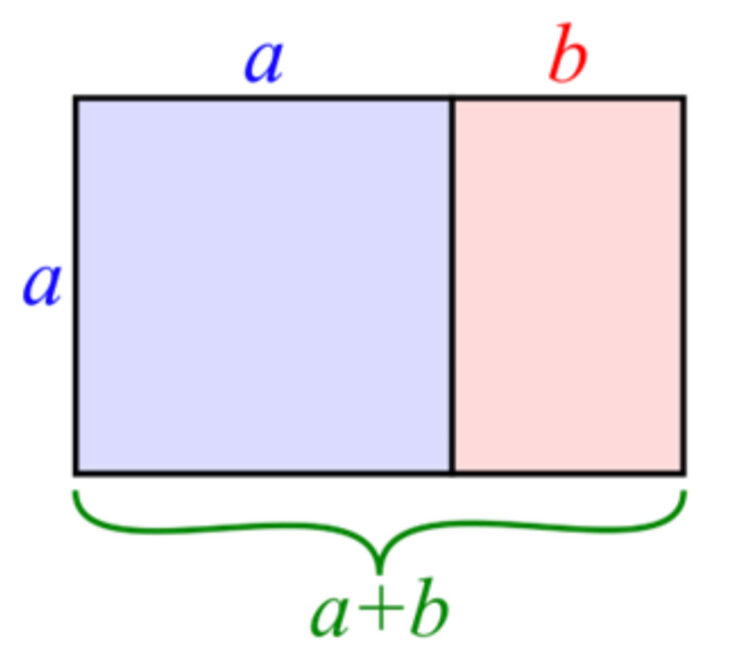
Den röda rektangeln har gyllene snittets proportioner b/a. Lägger man till en kvadrat på sidan a, så får man en större rektangel som också har det gyllene snittets proportioner. Tar man bort en kvadrat med sidan a, så återstår en mindre rektangel som också har det gyllene snittets proportioner b/a. Tar man sedan bort en kvadrat med sidan b från den mindre rektangeln, återstår en än mindre rektangel, fortfarande med gyllene snittets proportioner, o s v.
Löser vi ekvationen b/a = a/(a+b) (en s k andragradsekvation), får vi resultatet b/a, vilket är ungefär 0,618034.
Dessa proportioner sägs vara speciellt harmoniska och lär finnas på många håll i naturen. Till exempel ska naveln dela människans kropp i ett gyllene snitt. Det är bara att mäta. Lämpligen på en av de många bilder av fysiska praktexemplar som huserar på tidningarnas sport- och nöjessidor.
Svenska flaggan har proportionerna 5:8, alltså 0,625. Ganska nära gyllene snittets 0,618. På längden delas den i förhållandet 3:5 = 0,6. Även detta nära gyllene snittet.

USA:s flagga har förhållandet 10:19 mellan höjd och längd. 10/19 = 0,526.

Detta är alltså den flagga som vajar från regeringsbyggnader, ambassader, krigsfartyg etc. Flaggor som privatpersoner köper och hänger upp kan däremot se ut lite hur som helst, men ofta har de måtten 3:5, alltså betydligt närmare gyllene snittet. Om dessa mer harmoniska proportioner än regeringens har någon filosofisk eller politisk betydelse låter jag vara osagt.
Hur är det med ishockeyrinkar?
Den europeiska är 30×60 meter och den ”olympiska” 30,5 x 61 meter (100 x 200 fot), obetydligt större men båda långt från något gyllene snitt. Men så är ju inte heller ishockeymatcher några harmoniska tillställningar. Den nordamerikanska NHL-rinken är lika lång men nästan fem meter smalare än den olympiska (85 x 200 fot). Spelet blir därefter. På nyare skridskoanläggningar brukar det finnas en olympisk rink sida vid sida med NHL-rinken.
A4-formatet är sådant att om man klipper arket mitt itu får man två A5-ark med samma proportioner mellan sidorna som A4. Det betyder att sidorna måste förhålla sig som ett till roten ur två, alltså 0,707 ungefär.
I USA motsvaras A4 av ”letter-size”, lite kortare och bredare än ett A4-papper. Här gäller ANSI, American National Standards Institute, i resten av världen ISO, Internationella Standardiserings-Organisationen. Sagan om våra pappersformat berättas på ett fantasieggande sätt av bilden nedan. Men flera frågor inställer sig. T ex är det något lurt med formatet på A1. 594 gånger roten ur två är ju 840,0 och inte 841 som påstås. Den uppmärksamme betraktaren finner lätt flera andra konstigheter.

De gamla grekerna löste inte andragradsekvationer som vi utan använde geometriska metoder. Närmare bestämt med hjälp av två verktyg: passare och ograderad linjal.

Så här kunde gyllene snittet konstrueras:
Drag först en godtycklig horisontell sträcka (AB) och därefter en hälften så lång sträcka (AC) vinkelrätt mot den första. Som sidorna i en olympisk hockeyrink, alltså. Fullborda sedan triangeln genom att dra diagonalen (triangelns ”hypotenusa”).
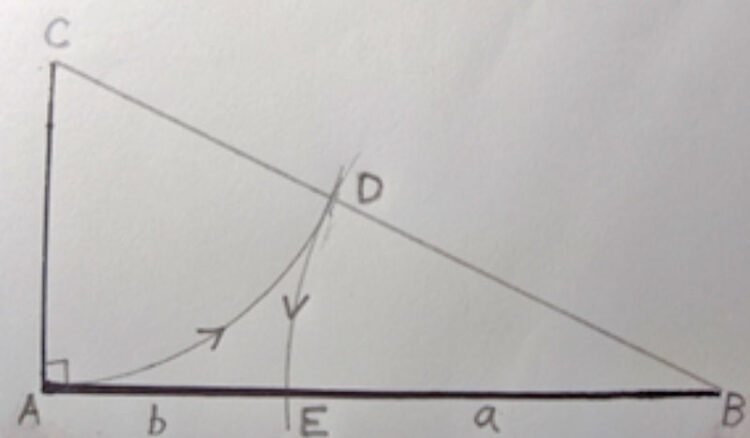
Sätt passarspetsen i C och drag en cirkelbåge från A till hypotenusan, som den skär i punkten D. Sätt sedan passarspetsen i B och drag en cirkelbåge från D till sidan AB som träffas i punkten E. Punkten E delar sträckan AB i det gyllene snittet:
b/a = a/(a+b)

Därmed har vi alla ingredienser som behövs för att konstruera ett pentagram (pentagon är en regelbunden femhörning).
Rita först en cirkel med radien a+b, dvs sidan AB i triangeln ovan. Drag sedan en cirkelbåge med radien a och centrum i B enligt figuren nedan. Förläng radien så du får diametern BM. (Händelsevis är sträckan a sidan i en regelbunden 10-hörning, som kan inskrivas i cirkeln. Därför är sträckan FG sidan i vår femhörning.)

Drag nu en linje från F genom E till K och en annan från G genom E till L. Förbind M med F och G.
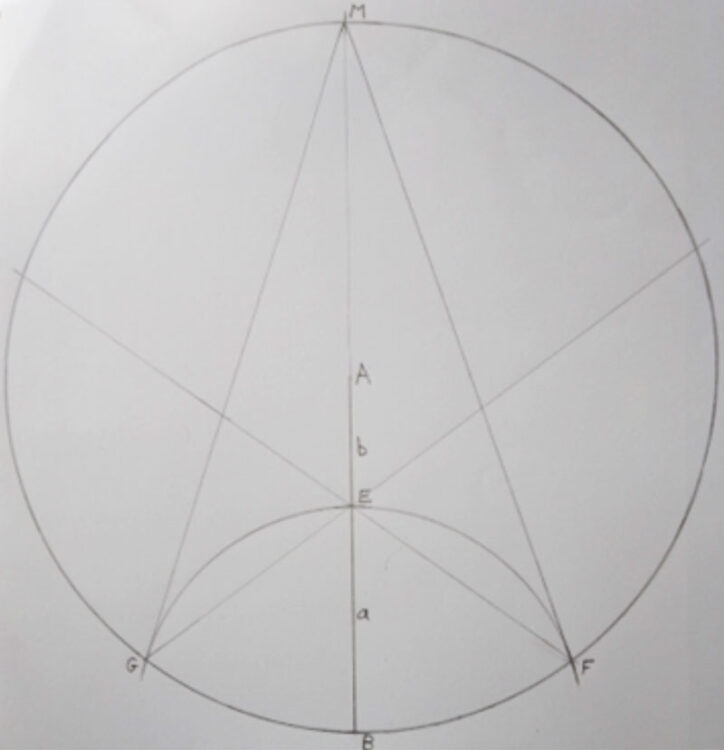
Därmed återstår bara linjen från K till L och pentagrammet är klart:

Av dessa stjärnor finns alltså 50 styck på USA:s flagga. Tio gånger så många som på folkrepubliken Kinas!
Lite tydligare:
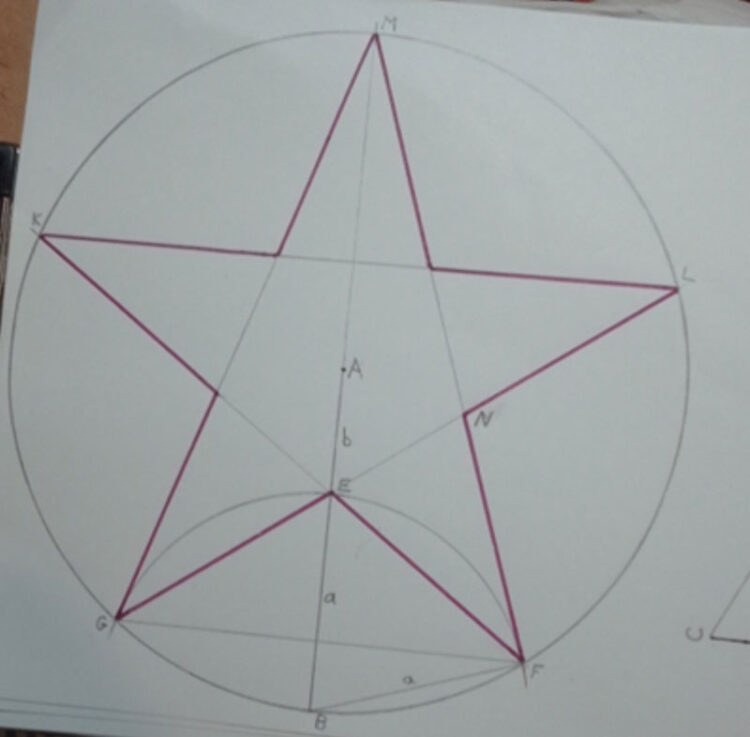
Ju mer jag stirrar på pentagrammet, ju mer harmonisk känner jag mig. Det beror på att det innehåller ett otal gyllene snitt.
Punkten E i figuren delar t ex sträckorna GN, GL, EL, EF, FK, samt den vi startade med, AB i gyllene snittet. FG förhåller sig till FM som gyllene snittet.
Vän av ordning undrar säkert vad meningen med dessa figurer är. Vad är sensmoralen av dessa konstruktioner och vilka slutsatser kan vi dra? Svaret är: Det finns ingen sensmoral, och inga slutsatser kan dras. Är det någon mening alls med att sitta och rita dessa figurer, så är den att man får lite kunskap om geometri, vilken sedan kan användas till att skaffa sig mer kunskap om geometri.
Tycker man illa om geometri kan man i stället använda Fibonaccis talföljd för att få fram ett noggrant siffervärde på gyllene snittet. Talföljden börjar med 0 och 1 följda av 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 o s v. Alltså 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … Dividerar man ett tal med det följande blir resultatet allt närmare gyllene snittet, ju högre upp i talföljden man går: 3/5 = 0,6. 8/13 = 0,615…, 89/144 = 0,618…
Fibonacci är värd några ord. Född i Pisa, Italien omkring 1170, undervisades han av arabiska lärare i nuvarande Algeriet, dit familjen flyttat. År 1202 publicerade han boken ”Liber Abaci”, där han introducerade det ”indiska systemet”, eller vad vi nu lite slarvigt brukar kalla de arabiska siffrorna till det medeltida Europa. Den mest revolutionerande av dessa siffror var nollan. Någon nolla finns som bekant inte bland de hopplösa romerska siffrorna. En gamling som aldrig läste latin på gymnasiet undrar ödmjukast hur kejsar Nero och alla hans konsuler och 38 vasaller uttalade ”trettioåtta”, alltså 3×10 + 8. Själv har jag väldigt svårt att uttala ”XXXVIII”.
I boken ställer han (Fibonacci alltså) upp ett problem om hur en population av kaniner ökar under vissa ideala förutsättningar (bl a massiv inavel kombinerad med odödlighet). Lösningen var den talföljd som långt senare fick hans namn. Men i Indien var den känd redan på 500-talet e kr. Hur som helst anses han vara medeltidens störste matematiker. På 1980-talet gav han t o m namn åt ett punkband i Los Angeles, The Fibonaccis. Deras musik beskrevs som ”elevator music from Hell”. Berömdare än så kan en matematiker knappast bli.









